I’m moving this site to http://holdenlee.github.io/blog. All posts on this blog will remain here, but the site will no longer be updated.

Also check out my new writing project at Philosophocle.

I describe some of my reasons for the move in my first post. I’ve enjoyed blogging with WordPress, but it’s come time for me to graduate and manage my own blog, built using Hakyll. I’ve prioritized functionality over design, and am still in the midst of setting it up, so the road ahead may be a bit bumpy, but I’m excited.

Thanks for reading my blog, and I hope you will join me in this new chapter!

New: I created a shared workflowy for sharing notes that I take. (I put in some notes on linguistics and neural nets.)

(h) means personal highlights.

• Books I read this year
• Don’t let the energy escape
• A beautiful implementation of Conway’s Game of Life and variants
• Hitchhiking robot meets its end in Philadelphia.
• I’ve started using Feedly to get all the blogs, etc. I subscribe to in one place. (Here’s a list of all the apps/extensions I use.)
• Plover is an open-source stenography engine. Stenography is a way of typing ultra-fast (experienced stenographers can do 200+ words a minute) by “chording” – pressing multiple keys at once. The learning curve is rather steep though.
• Movies: I’ve watched a bunch of movies (free trial of Amazon prime). Here are some I’ve enjoyed:
  • Song of the Sea – beautiful animated film with Irish mythology
  • Pulp Fiction – iconic American classic
  • The Kid – Charlie Chaplin!
  • Dr. Strangelove: How I Learned to Stop Worrying and Love the Bomb – dark Cold War humor
  • Lawrence of Arabia – Epic, classic
  • Little Women – a heartwarming classic of 4 sisters growing up
  • The Royal Tenenbaums – Wes Anderson humor
  • Astro Boy – Animated sci-fi
• Math
  • Tie a string to the lower pedal of a bike when the pedals are vertical, and pull backwards. Which way does the bike go? Answer.
  • I learned about this through Mathematical Understanding of Nature by Vladimir Arnold – a gem of a book.
  • Math books in dialogue/story form
  • Rosetta stone of Category Theory in physics, topology, logic, and computer science – I found this very illuminating.
  • A mathematician’s New Year’s resolution (humorous)
  • Quanta magazine about math and science
• Rationality
  • Common knowledge and Aumann’s Agreement Theorem
  • Fundamental ideas
  • A rationality/personality test
• Linguistics and related diversions
  • I learned a little bit of linguistics from An Introduction to Linguistics (which also has a lot of nice wordplay!) and Contemporary Linguistics. (notes on workflowy)
  • Lojban is a constructed language that’s designed to be very logical. I went through a few lessons in this tutorial. Some aspects are reminiscent of functional programming (ex. switching the order of arguments). The Haskell Wiki has a page on Lojban. I read a post that claims the analogy Lojban:Haskell::Esperanto:LISP.
  • The Language of Mathematics: because mathematical language is more precise than natural language, it’s a great area to apply linguistics to. It also pulls in ideas from computer science, in particular, type theory.
  • An online book on natural language processing.
• Programming
  • The connection between linguistics and math/programming languages is interesting and underexplored. Here are some discussions/articles I found:
    • Sociology of programming languages (h). See also this.
    • It’s hard to get a programming language to catch on! (Should this be more of a concern? (h)) In Confessions of a used programming salesman, Meijer tells his story of trying to sell Haskell to the masses. He realizes that the “change function”  is (Perceived Crisis/Perceived Pain of Adoption); you can’t just “build it and they will come.” Worse is better (h) is (controversial) assessment of the “failure” of LISP.
  • Learned a little bit of LISP after reading a lot of discussion on Haskell vs. LISP and metaprogramming:
    • LISP vs. Haskell 1 (h), 2
    • On metaprogramming 1, 2, 3
    • Metaprogramming in Haskell
    • Beating the average (with a better programming language, in this case, LISP) (h)
    • Paul Graham’s book On Lisp http://www.paulgraham.com/onlisp.html is a classic.
  • Extensible effects: I’ve read in several places that extensible effects are better than monad transformers (ex. cleaner, faster code), but it seems that it isn’t yet mainstream. A walkthrough of the code.
  • The Monad Tutorial fallacy: In teaching an abstract concept, the examples are more important than the metaphor.
  • I wrote a CYK parser in Haskell.
• Reasons to be Cheerful by Greg Egan (short story) – on being controlled by, or controlling, or own happiness.
• Podcasts
  • Fountain drinks (99PI) – Be thankful for water fountains!
  • Santa for president (The Truth)
  • Left Right Black White (Strangers) – Video games can help you get tenure and make friends!
  • Headspace, Just a little nicer (TED Radio hour)
• On Xunzi (Chinese philosopher) (h) Some excerpts
  Chinese philosophy was remarkably advanced at 300BC. Philosophers were revered in ancient China, and had a large part to play in developing the law and government. Some of Xunzi’s teachings included learning from the masters, the idea that all races are equal at birth and people developed differences from cultural upbringing, the notion that praying to heaven has no effect, and a the idea that all humans have core and irreducible desires, one of which is a desire for social position. The difference between the virtuous and petty man lies in how they achieve it -through loyalty and filial piety, or by impressing others.

1

You’ll be captain, you said, and I’ll be first mate.
I’ll ask you questions, you give me answers, and I’ll be the devil’s advocate.

(goodreads, detailed notes)

Saskia thinks of Thomas, walking inland with his oar on his shoulder. He walked until no one knew him or his people, until he was so much a stranger in a strange land that the man at the gate mistook his oar for a winnowing fan. What would Saskia’s “oar” be?

The Saskiad is a rite-of-passage story written in stream-of-consciousness. It’s about imagination, the desire to explore the unknown, the beautiful illusion of pinning fantasy over reality, contradictions of character, and the meaning of home and family.

It’s part of a small genre of books which have a powerful effect on me: The Slow Regard of Silent Things, The Grasshopper King, The Perks of Being a Wallflower, The Curious Incident of the Dog in the Night-time. These books appeal to me because they’re all about people who don’t fit in but/because they have a rich life inside their head. It’s compelling to see how deep the arrow of a thought can go.

(Warning: Spoilers and sexual references.)

Robert Sedgewick, professor of computer science at Princeton, gave a talk on Thursday on “Computer Science for the Masses,” outlining his vision for education in the future. He used as example his experience in turning the introductory CS course and algorithms course at Princeton into a MOOC and a “blended” course at Princeton. You can browse his courses on Coursera.

Notes I took during the talk are available here.

I’ll summarize some of the key points from his talk, reorganized for clarity. First, I’ll give some background, introduce the benefits of online education, and frame the question of how to blend it with traditional education. Next, I’ll give Sedgewick’s model of what an online course should look like: how to actually go about making one? Finally, I’ll outline his vision for the future of education. To distinguish my points from his, I’ll put my own thoughts in brackets.

 

• I moved my website to http://holdenlee.github.io. I’m using tiddlywiki, which has many cool features like filtering and transclusion.
• I learned the Tokyo (Ievan) Polka dance from Jacob Cole. Song (Miku version, traditional version).
• Math and computer science
  • What’s a mathematician to do? (If you can’t make a “significant” contribution, what’s the point?)
  • Mathematical microagressions, Francis Su We should be mindful of the language we use when teaching mathematics. Here, microagressions refer to common verbal or behavioral slights that can communicate to students “you don’t belong in mathematics.” (Ex. use of “obvious/clear/trivial”) Really, it’s good to have this kind of mindfulness in any interaction.
  • Graph Isomorphism is solvable in Quasi-polynomial time: exposition, talk
  • Neural nets
    • From Chris Olah’s blog:
      • Introduction to LSTM’s, with clear diagrams  [h]
      • Neural nets from a functional programming viewpoint
      • A Haskell package for building neural nets (Andrew Tulloch)
    • From Andrej Karpathy’s blog:
      • Cool visualizations and examples of RNN/LSTM output
      • Short science fiction story on neural nets
      • What neural nets think about your selfie
• Programming
  • Web scraper in Haskell
    • I learned how to build a web  scraper in Haskell: http://adit.io/posts/2012-03-10-building_a_concurrent_web_scraper_with_haskell.html
    • I want to build a scraper for a blog/wiki that will display as a graph how all the different posts are connected to each other. Here’s a simple program to scrape the links off the polymath 9 wiki: https://github.com/holdenlee/blographer
    • Which library to use? http://stackoverflow.com/questions/4838138/web-scraping-with-haskell
  • Blogs
    • Unknown Parallel, including a post on Tardis (the Dr. Who telephone box) in Haskell, lambda case (a shorthand for “f x = case x of…”)
  • Functional reactive programming (signals to deal with inputs, graphics, etc.): I’ve done this in Elm, and am looking at how to do it in Haskell.
    • Explanation of FRP using reactive-banana (reactive-banana)
    • I coded up Sokoban in Elm and Haskell using Helm. I documented the arduous process of installing Cairo (graphics library) and Helm here. (I don’t actually recommend Helm because not mature yet – there are various dependency problems. See…)
    • A comparison of FRP libraries in Haskell.
    • An actual game coded in Haskell!
  • Theory
    • Status quo of category theory and monads in TCS (stackexchange)
    • The Little Prover, a book about implementing a theorem-prover from scratch. I like the pedagogy of the series (The Little LISPer/Schemer/Prover) – all the books are written in 2-column Q&A format.
    • Type theory
      • PL zoo, an implementation of a variety of baby programming languages
      • How to implement dependent type theory (OCaml)
      • I finally coded up Hindley-Milner type inference, drawing heavily on Write You a Haskell (my code is not so beautiful)
      • I browsed Types and Programming Languages, Benjamin Pierce (from this recommendation)- it gives a good foundation for understanding different type systems (cleared up a lot of things for me) and I wish I’d picked it up earlier.
  • Getting the type of a variable at runtime: 1, 2
  • Folds and catamorphisms
• I went to a talk by Larissa MacFarquhar on her book Strangers drowning (Notes, incomplete because my laptop ran out of battery). What struck me was how complicated the idea of altruism has become over the past century. With the disaster of communism, the rise of capitalism (and ideas from people like Ayn Rand), there’s a pallor of suspicion surrounding the term altruism.
• Podcasts
  • RadioLab: Update: New Normal? Story of the first transgender mayor in the US (sometimes a small town can be the most progressive place), what baboons tell us about the role of nature vs. nurture in violent behavior, the side effects of domestication (it basically makes foxes not grow up)
  • Strangers: A portrait of the artist as a young woman – a story about an Arizona dream-turned-nightmare
  • This American Life: The Leap (transcript)
  • TED Radio hour
    • Quiet
      “Western societies, and in particular the U.S., have always favored the man of action over the man of contemplation. But in America’s early days, we lived in what historians call a culture of character where we still at that point valued people for their inner selves and their moral rectitude.” Susan Cain
      “It’s impossible to stutter when you sing.” Megan Washington
• Current events
  • Paris and memetic immunity Wars are fought not just with weapons, but with stories. But the solution isn’t just to force-feed our own stories. We need to educate people to evaluate the stories that they hear and form their own narratives – but that’s very difficult.
  • It’s disappointing how few states are accepting Syrian refugees. An apt comparison with our history.
  • There’s been a wave of race-related protests starting from Missouri, including Occupy Nassau (results?). And a protest against protests: “College is the last place that should be a safe space“
  • My white neighbor thought I was breaking into my own apartment. Nineteen cops showed up.
  • The Onion: Historians Politely Remind Nation To Check What’s Happened In Past Before Making Any Big Decisions
• Literature
  • Figments, Princeton’s speculative fiction magazine. My favorite is Ivory by Thomas Garcia, a satire of prestigious institutions (like Princeton…) “They mistook conformity for success, and success for vitality, and in their disillusionment they would become victims of Ivory’s education. She knew the game, and played it.”
  • Leviathan Wakes, James Corey – space opera, plot is amazing and unpredictable. There are some incidents that instigate hostilities among Earth, Mars, and the Belters and make people clamor for war – it feels like a scary parallel to today’s world.
  • The Saskiad, Brian Hall – one of my favorite books now. (Post on this coming.)
  • currently reading Wild Swans, Jung Chang – nonfiction, story spanning 3 generations in China (WWII, the Cultural Revolution…). It’s books like this that make me think that real history can be crazier than anything people can make up.
• Movies
  • Eternal Sunshine of the Spotless Mind – beautiful movie in a future where people can erase each other from their memories. (Summary/quotes)
  • Where are the Dreams of Youth? – Japanese silent film with orchestration, as part of the Rocky film forum. How corruption destroys friendships. Powerful scene at the end: “Remember that these punches are a token of our friendship.”
• Economics: Keynesian beauty contest, Guess 2/3 of the average (Try this game before you read)
• Apps, extensions, shortcuts
  • Cogi – record just the highlights of a lecture, conversation, etc.
  • Lock tab
  • Windows keyboard shortcuts

 

Books

Links (*found especially interesting, [h] personal highlights)

• It’s decorative gourd season, motherfuckers! http://www.mcsweeneys.net/articles/its-decorative-gourd-season-motherfuckers
• *Winnowing Oar – some penetrating posts: http://celandine13.livejournal.com [h]
• Some links followed from Winnowing Oar
  • Ivy League’s Failure Is Wall Street’s Gain http://www.bloombergview.com/articles/2012-02-16/harvard-liberal-arts-failure-is-wall-street-gain-commentary-by-ezra-klein [h]
  • Filthy Lucre http://www.vice.com/read/filthy-lucre ((1) Getting rich is not correlated with “deserving” it, but with playing a certain game. (2) Money helps in doing things you want. It really does.) [h]
  • *Unified theory of nerddom: http://theviewfromhell.blogspot.com/2012/09/trying-to-see-through-unified-theory-of.html [h]
• Pick-up artists – did not know this was a thing. https://en.wikipedia.org/wiki/Seduction_community https://en.wikipedia.org/wiki/The_Game:_Penetrating_the_Secret_Society_of_Pickup_Artists
• LessWrong
  • *Tell culture: http://lesswrong.com/lw/jis/tell_culture/
  • Developing habits on the 5-second level: http://lesswrong.com/lw/5kz/the_5second_level/
• A fervent defense of frequentist statistics: https://jsteinhardt.wordpress.com/2014/02/10/a-fervent-defense-of-frequentist-statistics/
• Blog on the Iraq war http://riverbendblog.blogspot.com/
• The We Speak survey at Princeton: It’s great that Princeton gave a survey on sexual assault, right? Actually, Princeton refused to take the standard survey, making the results “not directly comparable,” because they wanted one that’s tailored to itself.
  • http://www.universitypressclub.com/archive/2015/10/why-didnt-princeton-take-the-aau-survey-on-sexual-assault/
  • https://www.princeton.edu/main/news/archive/S44/35/32C48/index.xml?section=topstories
  • http://dailyprincetonian.com/opinion/2015/04/editorial-take-the-wespeak-survey-its-a-princeton-issue/
• http://dailyprincetonian.com/news/2015/05/10-years-after-founding-anscombe-society-sparks-debate-over-sexual-ethics-free-speech/
• A storytelling game: http://agentyduck.blogspot.com/2015/10/pantheon.html
  • Looks like a promising way to hone creative writing skills: http://writerkata.com/
• Programming-related
  • Proofs as stories http://wadler.blogspot.co.uk/2014/02/off-beaten-track-3-proofs-as-stories.html
    • *Building smart interactive fiction systems http://versu.com/
    • Explanations at https://emshort.wordpress.com/ (Ex. Conversation structure)
  • Haskell
    • Free monads
      • http://www.haskellforall.com/2012/06/you-could-have-invented-free-monads.html
      • Free monads and category theory http://www.paolocapriotti.com/blog/2013/11/20/free-monads-part-1/
    • Freer monads (an alternative to monad  transformers) https://www.reddit.com/r/haskell/comments/3joxd7/freer_monads_more_extensible_effects/
    • Understanding weak head normal form http://stackoverflow.com/questions/6872898/haskell-what-is-weak-head-normal-form
    • Different kinds of folds https://wiki.haskell.org/Foldr_Foldl_Foldl’ http://stackoverflow.com/questions/33006372/laziness-of-in-folding
  • Bayesian stats for programmers: http://camdavidsonpilon.github.io/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/
• Godel’s lost letter (my favorite theory CS blog)
  • *A model of human chess performance https://rjlipton.wordpress.com/2015/10/06/depth-of-satisficing/
  • https://rjlipton.wordpress.com/2015/10/12/is-the-hot-hand-fallacy-a-fallacy/
  • https://rjlipton.wordpress.com/2015/09/24/frogs-and-lily-pads-and-discrepancy/#more-12828
  • https://rjlipton.wordpress.com/2015/06/25/we-say-branches-and-you-say-choices/
  • https://rjlipton.wordpress.com/2012/03/24/interdisciplinary-research-challenges/
  • https://rjlipton.wordpress.com/2015/08/14/cryptography-and-quicksand/
  • https://rjlipton.wordpress.com/2012/12/19/branch-and-bound-why-does-it-work/
  • https://rjlipton.wordpress.com/2010/10/23/galactic-algorithms/
• Your nightmare stories of working for a tech giant: http://gizmodo.com/your-nightmare-stories-of-working-for-a-tech-giant-1736103312
• 4 rituals to make you happier: http://www.businessinsider.com/a-neuroscience-researcher-reveals-4-rituals-that-will-make-you-a-happier-person-2015-9

Other media/activities

• Went to the monthly open mic night (The Hallows) at Princeton and really liked it. https://www.facebook.com/events/756574911121073/
• Reading Leviathan Wakes
• Podcasts
  • Working my way slowly through The History of Rome
  • Review the future
    • 67 Cryogenics
    • 48 Should we have control over our consciousness
• Watched and enjoyed
  • A Comedy of Tenors at McCarter
  • Ph.D. Movie 2
• Started playing English Country Tune (puzzle game)

Wymar was the city of wind. It was nestled between hills. Each house had a weathervane, with some icon that glinted in the sun: a silver lark, a spinning solar system, a blue-and-white teacup that crawled with Sina-style dragons, a whale, a bionic dancer in heels. They swiveled and creaked. Laundry fluttered on lines that were weighed down with round, golden ornaments in the shape of fruit. Shirts and underpants were clipped on with steel teeth.

Keep reading (on googledocs)…

This is a chapter of the novel I was trying to write last November. The novel fell apart, but this is one part I really liked (and is seasonally appropriate!), so I thought I’d share it. This is pretty much the raw version, with minimal edits. (There’s background in the linked post, but it isn’t too helpful. All you really need to know is that Linus and Zeo are the main characters, their bots are Linx and Argon, and they’re touring the world.)

I gave a talk on Tuesday at the “Gems of Theoretical Computer Science” seminar on the LLL algorithm.

Abstract:

The LLL (Lenstra–Lenstra–Lovász) algorithm is a lattice reduction algorithm that can approximate the shortest vector in a lattice, and has numerous applications (which I’ll cover as time permits), including polynomial-time algorithms to

• factor polynomials over the rationals
• given an approximate root of a low-degree rational polynomial, recover the polynomial
• find integer relations such as
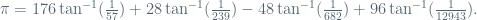
• solve integer programming in fixed dimension
• break certain cryptosystems.

Notes from the talk are here (TYPO on pg. 3: the example at the bottom should be [[1, .3, 4.2], [0, 1, -.3], [0,0,1]] -> [[1, .3, .2], [0, 1, -.3], [0, 0, 1]]. I didn’t get to cover all topics). Quick summary:

• The goal is to find the shortest vector in a lattice. The LLL algorithm draws inspiration from 2 simple algorithms, the Euclidean algorithm (1-D case; it has a “reduce” and “swap” step), and the Gram-Schmidt orthonormalization process (to generalize to higher dimensions). A reduced basis comes “naturally” from making an algorithm that does a “reduce” and “swap” steps. The LLL algorithm only gives an exponential approximation, but this is good enough for many purposes.
• The algorithm terminates because smaller vectors filter to the front; create a invariant out of that.
• A closely related problem is the Closest Vector Problem. Solve it by moving the point to a fundamental parallelopiped of the reduced lattice.
• The LLL algorithm can be used to find integer relations between numbers given sufficiently good approximations. Applying this to powers of an algebraic number, we can recover the minimal polynomial. Applying this to roots of a polynomial we can factor the polynomial.
• The algorithm for Closest Vector can solve Integer Programming in fixed degree, by recursion on the dimension. Bounds on the size of the basis elements in a reduced basis bounds the number of hyperplanes cutting the convex set.
• LLL can break RSA with small exponent by finding roots of polynomials mod N of small degree.

Some more resources are the following:

• Oded Regev’s course on lattices in CS (main reference)
• Jonathan Kelner’s class at MIT
• Phong Nguyen’s slides
• Original LLL paper
• Mathematics by Experiment: algorithms similar to LLL are used in math to do things like find crazy-looking identities.

*Found particularly interesting.

Links and readings

• Podcasts
  • *Sexistential (Strangers) – An eye-opening documentary, and probably not what you are expecting – Main idea: with society’s contradictory attitudes on sexuality, there is no safe space for people to learn about sex. This is where Kendra Holliday, sex surrogate, steps in.
  • *Darkode (RadioLab) – Large-scale organized Internet crime.
  • Enjoy the Suffering (The Truth) – A story about Hell
  • This American Life
    • The Land of Make Believe – A father constructs an elaborate fantasy ship in to occupy his 12 children.
    • What’s Going On In There? – An abusive relationship; a son and father who can’t understand each other’s languages.
    • Too Soon? – On the making of a reality show featuring OJ Simpson.
  • The Source of Creativity (TED Radio Hour) – Drawing creativity from empathy with others, studying the brain during creative activity (jazz improvisation). Interesting: Creativity comes from turning off the part of your brain that self-reflects.
  • 99% Invisible
    • 180 Reefer Madness – Someone had to invent shipping containers! When you add refrigeration, things become more complicated.
    • *179 Bathysphere – People only found out there was life in the deep sea when they found transatlantic cables covered with critter remains. On the wondrous journey of the first attempt to explore the deep sea, in a “bathysphere.”
    • 177 Lawn Order – On the responsibility to maintain (or not maintain?) your lawn.
  • *IndieFeed – Performance poetry podcast. Too many wonderful poems to list individually, go check them out!
• Media
  • Neurotic Neurons, Nicky Case – an animation on Hebbian learning and its relation to behavioral psychology
• Slam poetry
  • Andrea Gibson
    • *Asking too much (words)
    • Maybe I need you 
    • Letter to the playground bully (words)
  • *The Type, Sarah Kaye 
  • *Unrequited love poem, Sierra DeMulder 
  • *Repetition, Phil Kaye 
  • *Unsolicited Advice to Adolescent Girls with Crooked Teeth and Pink Hair, Jeanann Verlee 
  • Somewhere in America 
  • Rigged Game, Dylan Garity (NPS 2013) 

• Books
  • *The Slow Regard of Silent Things, Patrick Rothfuss – a beautiful and unconventional book, featuring one character and her relationship to the objects she finds and makes alive.And while her eyes were all softness and want, her mouth grew firm and furious. No. That was not the way of things. She knew better. She knew perfectly well where this sheet belonged… She was a greedy thing sometimes. Wanting for herself. Twisting the world all out of proper shape. Pushing everything about with the weight of her desire.
  • currently reading The Master and Margarita, Mikhai Bulgakov
• A few random posts/articles
  • Write, Arxiv, Repeat – how we can simplify researchers’ workflows
  • Why someone left academia
  • Water on Mars
  • Ignoring your passion is slow suicide
• Programming (I’m collecting Haskell links here.)
  • Learn You an Agda!
  • Type-level programming in Haskell
  • State of the Haskell ecosystem – What Haskell is good at, and where it needs work.
  • Write You a Haskell – A 100-page tutorial on writing a proto-Haskell compiler in Haskell. Some beautiful code here; it goes fast and teaches tons of stuff. Especially helpful for me were the nice examples on monad transformer stacks.
  • TypeFunc – Lots of links for resources on functional programming.
• *Julia’s links for September including a proposal to replace London’s Tube with moving sidewalks and a fully automated restaurant.
• Games I learned about
  • VVVVVV
  • I Wanna Be the Guy – The ultimate troll computer game. Look up “rage quit I wanna be the guy” on YouTube.

Activities

• I have a paper Quadratic polynomials of small modulus cannot represent OR on the arXiv.
• Simons meeting on Intractability in Machine Learning. Some (messy) scribed notes are here (source).
• For COS513 (Probabilistic Modeling) (links to projects) I’m working with Maxim Zavslavsky and Kevin Miller on modeling rats’ strategies for the “two-armed bandit problem.” See our blog.
• I auditioned for Ellipses (Princeton’s slam poetry team). I didn’t get in, but got exposed to some wonderful poetry, and found out about some literary/performance events that I’ll be going to: the monthly Butler Open Mic Night (next one: Nov. 13), and the open mic night at the Princeton Cemetery (next one: Oct. 30).
• I wrote a Sudoku solver and various search algorithms in Haskell. In both I aimed to write code that’s very general (ex. constraint propagation using the AC3 algorithm) rather than tailored to the specific problem at hand.